坚持做高胜率高赔率的操作

（原标题：坚持做高胜率高赔率的操作）

今天市场能走成这样已经不错了，上午10：30的时候跌的多的国证2000和科创50最大跌幅都在2%左右了。正当大家以为今天会再次大跌的时候，有一股神秘力量把大盘给拉起来了。

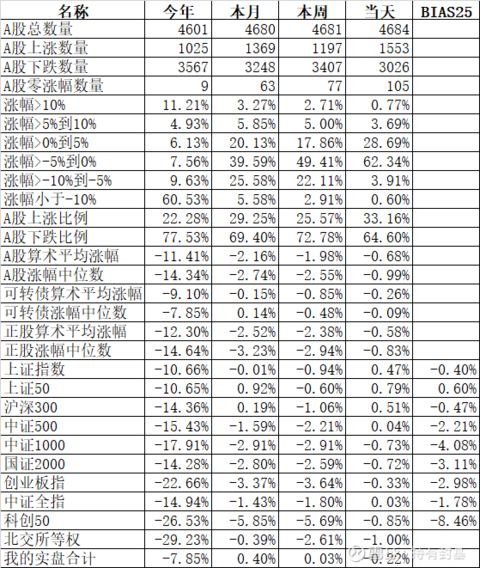
今天行业上领涨的还是工程机械、建筑、房地产等，不是受消息面影响的就是低估的板块。昨天房地产显然是上涨过程中的调整，跌了一天今天就大涨了2.85%。领跌的文教休闲、互联网、传媒娱乐等都是估值相对偏高的板块。这个季度的主线是价值板块而不是成长板块，不会受一两天的异常涨跌的影响。

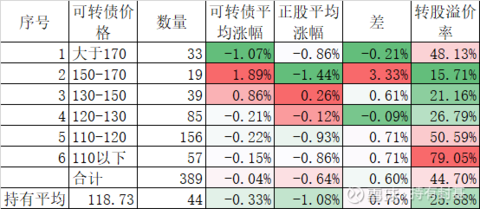
今天个股涨少跌多，64.60%的个股下跌，可转债的表现已经比个股好多了。今天我持仓的岩土转债的正股涨停，可转债截止到收盘也大涨了12.70%，我卖出去的时候虽然没那么高，但也涨了10.82%

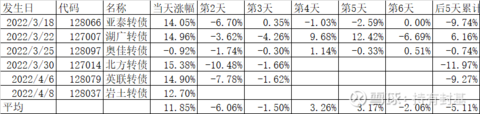
从3月18日开始每次卖出涨幅超过10%的可转债我都记录下来了，20天总共6次，其中奥佳我盘中涨了10%卖的，当天收盘跌0.92%，这样5天的平均超额收益最起码有6%。大概持有40只可转债，那么每次的贡献大概=6%/40=0.15%，一个月大概可以遇到9次，一年大概108次，不算复利0.15%*108=16.2%，已经相当不错了。

但这6次操作中，除了亚泰、奥佳成功的获取了10%左右的超额收益外，还有湖广踏空了大概6.16%，北方目前停牌，但2天避免了11.97%的下跌，英联2天避免了9.27%的下跌，岩土还不知道。6次里至少遇到1次失败的操作。如果是第一次操作遇到失败的踏空，很容易会被放弃了。

那怎么才能更加科学的去参与类似的操作呢？当年贝尔实验室物理学家约翰·拉里·凯利根据同僚克劳德·艾尔伍德·香农于长途电话线杂讯上的研究建立了凯利公式，从最初处理无线电信息到后来被用在赌局上，我们先来看一下公式：
F=（p*rw-q*r1）/（rw*r1）=p/r1-q/rw
F：应下注的比例
P：胜率
q：败率，=1-p
rw：获胜后的净盈利，
r1：失败后的净损失率

凯利公式明确的指出了下注的比例有个最佳值，超过或者小于这个最佳值的收益率都不是最高的。我们通过一个实际的例子会更加看的清楚：

假定有个赌局，盈利概率80%，盈利金额为2元。亏损概率为20%，亏损额为1元（本金亏光）那么按照凯利公式，应该每次下多少赌注呢：
F= p/r1-q/rw=80%/100%-20%/200%=80%-10%=70%。

如果参加5次，按照概率有4次赢1次输，那么这一次输如果发生在第一次，还是最后一次，对最后的结果有影响吗？

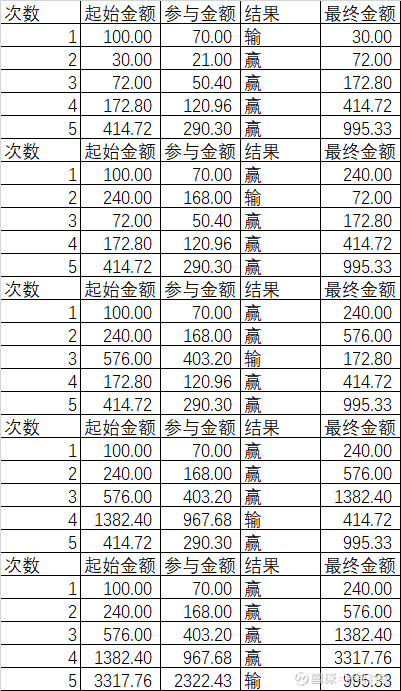
从上表的计算看到，不管这次输是发生在第一次，还是最后一次，或者是中间，对最后的结果毫无影响。但在实际中如果第一次输掉很容易中止

那我们再来看看，如果不是按照凯利公式的70%参与赌局，我们分别计算用50%、60%、80%、90%和70%对比一下，既然上面已经证明了输发生在任何一次对结果都无影响，那么我们统一假定第一次输：

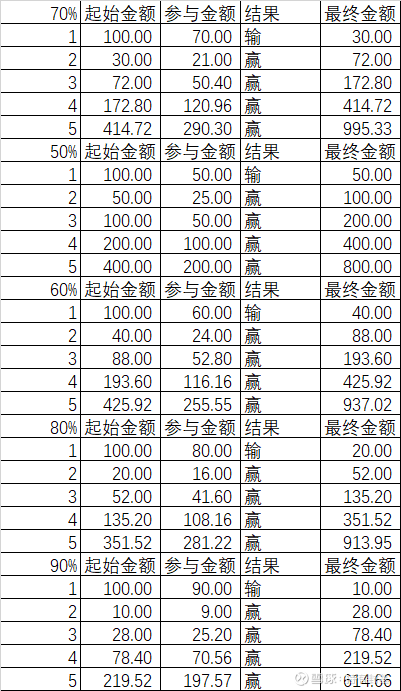
从上表我们可以看到，无论大于还是小于70%，最后的收益都比不过凯利公式得到的70%。
而且投注比例越接近最佳值，那么最后的盈利越高。

我们可以从凯利公式中学到科学的理智的参与类似赌局：
1、 胜率高的赌局，要高仓位参与；胜率低的赌局，要低仓位参与。
2、 盈利高的赌局，要高仓位参与；盈利低的赌局，要低仓位参与。
3、 不要输了一次就停止参与类似胜率和盈利的赌局，输赢发生的次序和结果无关。

特别是第三条，很多人会受最近一次输赢的影响特别大，最近一次赢了，会继续赌下去；最近一次输了，就停止了。如果你能大概率的知道胜率和盈利的，那么根据凯利公式，最终的结果和输赢的次序是无关的，唯一需要坚持的是自己的信念。

当然，在股市投资中比上述遇到的例子要复杂得多，而且输赢的多少事先也是不知道的。但遇到这样的操作机会，分散投资，坚持做高胜率高赔率的事情。不要去重仓或者满仓去赌一次机会。这是凯利公式给我们的启示。因为一次大的亏损，很容易终止这个游戏。就像著名投资人但斌今年在底部大幅度减仓，也是因为亏损多了逼近警戒线甚至清仓线。即使是你自己的投资，亏损严重到影响你的睡眠，就不是我们投资的初衷了。